Water Electromagnetic Flow Meter
Meter Data
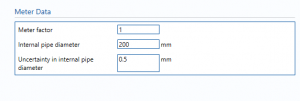
Meter factor – Enter the meter factor.
meter factor is ratio obtained by dividing the gross volume at standard conditions by the corresponding meter-indicated standard volume.
internal pipe diameter – Enter the internal diameter of the pipe.
Uncertainty in internal pipe diameter – uncertainty in the measurement of the internal diameter of the pipe.
Uncertainty parameters
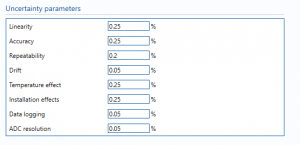
Linearity – The percentage uncertainty due to linearity. Linearity is calculated by getting the average and the range of the measurements made. The sample averages and ranges will be used with the reference values to determine linearity either graphically or by calculations.
Accuracy – The percentage uncertainty due to accuracy. Accuracy is the closeness of the measured value to the real value.
Repeatability – Percentage uncertainty in the reputability of the reading from the Water Electromagnetic Flow Meter.
Drift – Additional uncertainty allowance due to meter drift. Normally left at zero, unless evidence is present to suggest a higher value.
Temperature effect – The uncertainty in the reading due to the change in temperature.
Installation effect – The percentage uncertainty due to installation effects. Installation effects can be from several sources such as a distorted swirl in the profile of the flow due to the layout of the piping system.
Data logging – Uncertainty due to collection of data from different sensors over a period of time.
ADC resolution – The uncertainty due to the conversion of analogue signals to digital signals.
Uncertainty Budget
Volume flow rate
The uncertainty budget table shows a break down of the different components that contribute to the overall calculated uncertainty.
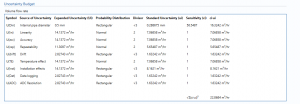
The values input into the uncertainty budget are derived from the inputs and uncertainty parameters. These values are taken in as the expanded uncertainties and are divided by a coverage factor to gain the standard uncertainty.
The coverage factor is determined by the probability distribution that best suits that uncertainty component. The standard uncertainty is then multiplied by the sensitivity value then squared. This is done for each component that contributes to the overall uncertainty in volume flow rate. The Standard Uncertainty in the volume flow rate is the square root of the sum of each component variance as shown in the following equation:
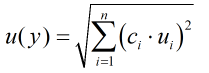
Mass flow rate
The uncertainty budget table shows a break down of the different components that contribute to the overall calculated uncertainty.
![]()
The values input into the uncertainty budget are derived from the inputs and uncertainty parameters. These values are taken in as the expanded uncertainties and are divided by a coverage factor to gain the standard uncertainty.
The coverage factor is determined by the probability distribution that best suits that uncertainty component. The standard uncertainty is then multiplied by the sensitivity value then squared. This is done for each component that contributes to the overall uncertainty in mass flow rate. The Standard Uncertainty in the mass flow rate is the square root of the sum of each component variance as shown in the following equation:
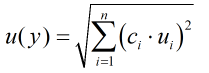
Calculated Uncertainty
![]()
The Expanded Uncertainty is the Standard Uncertainty multiplied by the coverage factor (k). The coverage factor is defaulted to k = 2 (equivalent to a confidence level of approximately 95%).
The Relative Uncertainty is the Expanded Uncertainty divided by the volume flow rate or mass flow rate depending on the parameter.
