Gas Density from MW
Description
This block calculates the uncertainty in Line and Standard density from Molecular Weight(MW).
Options
User selects if density is calculated or user entered.
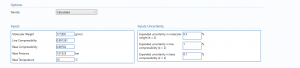
Note: As shown below, if user entered is selected then line density and standard density are entered along with their uncertainties.
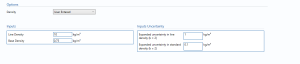
Inputs
Molecular Weight – the molecular weight of the gas.
Line Compressibility – is the compressibility factor for the on stream gas.
Compressibility Factor is the correction factor for the deviation of real gas from ideal gas behavior.
Base Compressibility – is the compressibility factor for the gas at standard conditions.
Base Pressure – is the pressure of the gas at standard conditions.
Base Temperature – is the temperature of the gas at standard conditions.
Inputs Uncertainty
Expanded uncertainty for molecular weight (k = 2) – the expanded uncertainty percentage in molecular weight calculation with 95% confidence level.
Expanded uncertainty in line compressibility (k = 2) – the expanded uncertainty percentage in the in line compressibility value with 95% confidence level.
Expanded uncertainty in base compressibility (k = 2) – the expanded uncertainty percentage in the in base compressibility value with 95% confidence level.
Calculations
Uncertainty Budget
Line Density
The uncertainty calculation is detailed in the uncertainty budget table giving a breakdown of how the overall uncertainty is calculated.
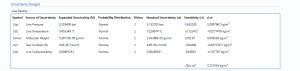
Uncertainties associated with these values are taken in as the Expanded Uncertainties. The Standard Uncertainty is calculated from dividing the Expanded Uncertainty by the coverage factor which is determined by the probability distribution that best suits that uncertainty component.
The Standard Uncertainty is then multiplied by the sensitivity value then squared. This is done for each parameter that contributes to the overall uncertainty in the line density. The Standard Uncertainty in the line density is the square root of the sum of each component variance as shown in the following equation:
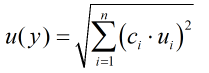
Standard Density
The uncertainty calculation is detailed in the uncertainty budget table giving a breakdown of how the overall uncertainty is calculated.

Uncertainties associated with these values are taken in as the Expanded Uncertainties. The Standard Uncertainty is calculated from dividing the Expanded Uncertainty by the coverage factor which is determined by the probability distribution that best suits that uncertainty component.
The Standard Uncertainty is then multiplied by the sensitivity value then squared. This is done for each parameter that contributes to the overall uncertainty in the standard density. The Standard Uncertainty in the standard density is the square root of the sum of each component variance as shown in the following equation:
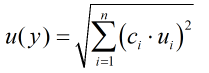
Calculated Uncertainty
![]()
The Expanded Uncertainty is the Standard Uncertainty multiplied by the coverage factor (k). The coverage factor is defaulted to k = 2 (equivalent to a confidence level of approximately 95%). The Relative Uncertainty is the Expanded Uncertainty divided by the line or standard density depending on the parameter.
References
Standards
ISO 5168:2005 – Measurement of fluid flow – Procedures for the evaluation of uncertainties
ISO Guide 98-3 – Uncertainty of measurement – Part 3: Guide to the expression of uncertainty in measurement (GUM:1995) (2008)