ECF
Description
This block calculates the uncertainty in the Energy correction factor for gas.
Options
![]()
Reference
- AGA 5
- ASTM D3588
- ISO 6976
- API MPMS Ch14.5/GPA 2172
This option determines which Reference is used for the calculation of Energy Correction Factor.
AGA 5
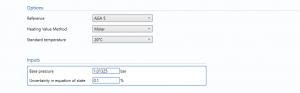
Heating Value Method
- Molar
- Volumetric
Select the method of calculation of the Heating Value or Calorific Value.
Standard Condition or Temperature
- 0℃, 100kPa
- 15℃, 101.325kPa
- 20℃, 98.0665kPa
- 59℉, 14.696psi
- 60℉, 14.4psi
- 60℉, 14.65psi
- 60℉, 14.696psi
- 60℉, 14.73psi
- 60℉, 15.025psi
Note: This is used if the Heating Value method is volumetric
or
- 0℃
- 15℃
- 20℃
- 25℃
- 60℉
Note: This is used if the Heating Value method is Molar
This option is used to determine the standard conditions or temperature used in the calculation.
ASTM D3588

Standard
- 1989
- 2000
- 2003
- 2009
Select the year of the reference standard to be used.
ISO 6976
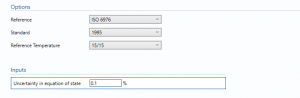
Standard
- 1983
- 1989
- 1995
Select the year of the reference standard to be used.
Reference Temperature
- 25/0
- 15/0
- 0/0
- 15/15
- 25/20
- 20/20
- 25/15
Reference Temperature for combusting and metering.
API MPMS Ch 14.5/GPA 2172

Base pressure
The pressure at base conditions.
Inputs
Uncertainty in equation of state
Uncertainty in the equation of state. Guidelines on determining this value can be found in the relevant standard.
Base pressure
The pressure at base conditions.
Note: This is used in the AGA 5 method if the Heating Value method is Molar or in the ASTM D3588 method.
Uncertainty Budget
The uncertainty calculation is detailed in the uncertainty budget table giving a break down of how the overall uncertainty is calculated. The values input into the uncertainty budget are taken from the module inputs and calculations from other blocks along with the uncertainty in the equation of state as input in this block.
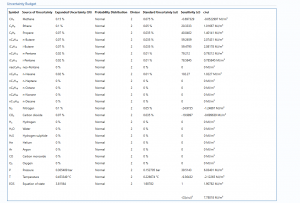
Uncertainties associated with these values are taken in as the Expanded Uncertainties. The Standard Uncertainty is calculated from dividing the Expanded Uncertainty by the coverage factor which is determined by the probability distribution that best suits that uncertainty component.
The standard uncertainty is then multiplied by the sensitivity value then squared. This is done for each parameter that contributes to the overall uncertainty in the Energy Correction Factor. The Standard Uncertainty in Energy Correction Factor is the square root of the sum of each component variance as shown in the following equation:
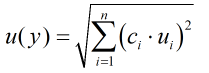
Calculated Uncertainty
![]()
The Expanded Uncertainty is the Standard Uncertainty multiplied by the coverage factor (k). The coverage factor is defaulted to k = 2 (equivalent to a confidence level of approximately 95%).
The Relative Uncertainty is the Expanded Uncertainty divided by calculated ECF.
References
Standards
ISO 5168:2005 – Measurement of fluid flow – Procedures for the evaluation of uncertainties
ISO Guide 98-3 – Uncertainty of measurement – Part 3: Guide to the expression of uncertainty in measurement (GUM:1995) (2008)
AGA Report No. 8 – Compressibility and Supercompressibility of Natural Gas and Other Related Hydrocarbon Gases (December 1985)
AGA Report No. 8 – Compressibility Factors of Natural Gas and Other Related Hydrocarbon Gases (2nd Printing July 1994)
ISO 12212-2:2006 – Natural Gas – Calculation of compression factor – Part 2: Calculation using molar composition analysis
KCCL Calculations
C156 – AGA8 1985/94 – Gas Density and Compressibility
