C271 – ISO 5167 – Venturi Mass Flow Calculation
Description
This calculates the mass flow rate for Venturi based metering systems according to the ISO 5167 standard.
References
ISO 5167: Measurement of fluid flow by means of pressure differential devices inserted in circular cross-section conduits running full
ISO TR 9464: Guidelines for the use of ISO 5167
Flow Measurement Engineering Handbook (2nd Edition) – R.W Miller
Kelton calculation reference C271
FLOCALC calculation reference K075: ISO 5167-1:1991 Venturi Calculation
FLOCALC calculation reference F076: ISO 5167:2003 Venturi Calculation
KIMS calculation reference K217: ISO 5167 Venturi Calculation
FLOCALC calculation reference F037: Upstream Density Calculation
Options
Standard Version
- 1991
- 2003
This option allows the selection of the version of the standard to be applied.
Fluid
- Gas
- Liquid
This option allows selection of whether the fluid in question is a liquid or a gas.
Discharge Coefficient
- User entered
- Variable with Reynold’s number
- Classical venturi with ‘as cast’ convergent section
- Classical venturi with rough-welded convergent section
- Classical venturi with machined convergent section
- Venturi nozzle
This option group allows the selection of Venturi type for the computation of discharge coefficient.
Exit Cone Angle
- 7°
- 15°
This option enables the selection of venturi exit cone angle which is used for the calculation of the permanent pressure loss.
Expansibility Factor
- User entered
- Calculated
This option gives the choice for expansibility factor to be entered by the user or calculated.
Temperature
- Upstream
- Downstream
This option allows selection of where the temperature is measured, upstream of the orifice plate meter or downstream where the flow has fully recovered. If the standard selected is 1991 the correction to upstream temperature will be isentropic, if the 2003 standard is selected an isenthalpic will be applied.
Joule-Thomson Coefficient
- User entered
- Calculated
This option group will appear if the 2003 standard and downstream temperature is selected, it allows the Joule-Thomson coefficient to be entered if the value is known or calculated by Reader-Harris’ simplified equation if otherwise.
Density
- Upstream
- Downstream
This option group allows selection where the density measurement is taken, upstream of the orifice plate or downstream at pressure, p2, and temperature T3. If the standard selected is 1991 the correction to upstream density will be isentropic, if the 2003 standard an isenthalpic will be applied.
Calculation
Mass Flow Rate
The mass flow rate is calculated by:
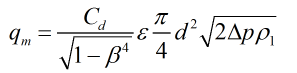
| Where | ||
|---|---|---|
| Cd | = | Discharge coefficient |
| β | = | Diameter ratio |
| ε | = | Expansibility factor |
| d | = | Venturi throat diameter |
| Δp | = | Differential pressure |
| ρ1 | = | Upstream density |
Discharge Coefficient
The coefficient of discharge is set at
- 0.984 for a venturi with ‘as cast’ convergent section
- 0.985 for a venturi with rough-welded convergent section
- 0.995 for a venturi with machined convergent section
For a venturi nozzle it is calculated from the equation
![]()
If the variable with discharge coefficient is selected a series of experimentally determined discharge coefficients with the accompanying Reynold’s numbers will be required to be input. An initial estimate of Reynold’s number will be used to calculate a discharge coefficient from the provided data using linear interpolation, from this mass flowrate is then estimated and then Reynold’s number. This forms an iterative loop to determine discharge coefficient, Reynold’s number and mass flowrate.
Expansibility Factor
The expansibility is calculated by:
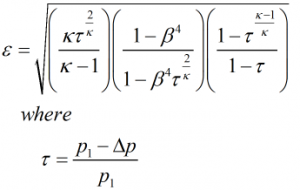
| p1 | = | Upstream pressure |
| κ | = | Isentropic exponent |
Pressure Loss
The permanent pressure loss equations used here have been taken from R.W Miller’s Flow Measurement Engineering Handbook
For a venturi with an exit cone angle of 7°
![]()
For a venturi with an exit cone angle of 15°
![]()
Temperature Referral
The temperature referral employed is the same as can be found here.
