C253 – AGA 8 – Gross Characterisation Methods
Description
This calculation uses either AGA8 Gross Characterisation Method 1 or 2 to calculate the compressibility factors and densities of dry, sweet natural gases at an alternative temperature and pressure.
References
AGA Report No. 8 – Compressibility Factors of Natural Gas and Other Related Hydrocarbon Gases. Catalog No. XQ9212 2nd Edition, 3rd Printing 2003
Kelton calculation reference C253
FLOCALC calculation reference F063
KIMS calculation reference K125
Options
Method
- Method 1
This option uses gross characterisation method 1 where volumetric gross heating value is used as an input parameter
- Method 2
This option uses gross characterisation method 2 where nitrogen content is used as input parameter
Choose option based on which input parameters you have. Note that the input value of gross volumetric heating value must be in energy per volume units e.g. MJ/m3.
Reference Conditions
- 0°C, 0°C, 1.01325 bar
- 15°C, 15°C, 1.01325 bar
- 25°C, 0°C, 1.01325 bar
- 25°C, 20°C, 1.01325 bar
- 60°F, 60°F, 14.696 psi
- 60°F, 60°F, 14.73 psi
- 60°F, 60°F, 15.025 psi
This option is available if Method 1 is selected. It allows selection of a variety of reference conditions relating to the heating value of the gas for both volumetric and molar values.
Constants
Gas Constant – R = 8.31451 J/molK
Molar mass of air – Mair = 28.96256 g/mol
Molar mass of nitrogen – MN2 = 28.01344 g/mol
Molar mass of carbon dioxide – MCO2 = 44.00964 g/mol
Interaction virial coefficient terms for nitrogen and carbon dioxide.
| Fluid for Bij | b0 | b1 | b2 |
|---|---|---|---|
| N2-N2 | -0.1446 | 0.74091 x 10-3 | -0.91195 x 10-6 |
| CO2-CO2 | -0.86834 | 0.40376 x 10-2 | -0.51657 x 10-5 |
| CO2-N2 | -0.339693 | 0.161176 x 10-2 | -0.204429 x 10-5 |
| Fluid for Cij | c0 | c1 | c2 |
|---|---|---|---|
| N2-N2-N2 | 0.78498 x 10-2 | -0.39895 x 10-4 | 0.61187 x 10-7 |
| CO2-CO2-CO2 | 0.20513 x 10-2 | 0.34888 x 10-4 | -0.83703 x 10-7 |
| CO2-N2-N2 | 0.552066 x 10-2 | -0.168609 x 10-4 | 0.157169 x 10-7 |
| CO2-CO2-N2 | 0.358783 x 10-2 | 0.806674 x 10-5 | -0.325798x 10-7 |
Virial coefficient terms for the equivalent hydrocarbon
| i | bi0 | bi1 | bi2 | |
|---|---|---|---|---|
| B0 | 0 | -0.425468 | 0.2865 x 10-2 | -0.462073 x 10-5 |
| B1 | 1 | 0.877118 x 10-3 | -0.556281 x 10-5 | 0.88151 x 10-8 |
| B2 | 2 | -0.824747 x 10-6 | 0.431436 x 10-8 | -0.608319 x 10-11 |
| i | ci0 | ci1 | ci2 | |
|---|---|---|---|---|
| C0 | 0 | -0.302488 | 0.195861 x 10-2 | -0.316302 x 10-5 |
| C1 | 1 | 0.646422 x 10-3 | -0.422876 x 10-5 | 0.688157 x 10-8 |
| C2 | 2 | -0.332805 x 10-6 | 0.22316 x 10-8 | -0.367713 x 10-11 |
Calculation
Gross characterisation methods 1 and 2 both use iterative procedures to calculate the compressibility factor at base conditions, composition of the mixture and the molar gross heating value of the equivalent hydrocarbon. This is then used to find the virial coefficients of the mixture.
The virial coefficients, B and C, of the mixture are found from:
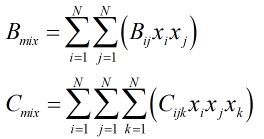
| Where | ||
|---|---|---|
| Bij | = | The individual components interaction second virial coefficient |
| Cijk | = | The individual components interaction third virial coefficient |
| xi,j,k | = | Mole fractions of respective gas components |
| N | = | Number of components in gas mixture |
Molar density, d, and compressibility factor, Z, are found from a further iterative process centred around the relationships:
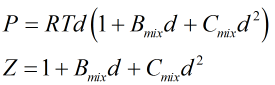
| Where | ||
|---|---|---|
| P | = | Absolute pressure |
| R | = | Gas constant |
| T | = | Absolute temperature |
| Bmix | = | Second virial coefficient of mixture |
| Cmix | = | Third virial coefficient of mixture |
The supercompressibility is then calculated by:
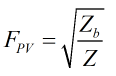
| Where | ||
|---|---|---|
| Zb | = | Base compressibility |