C192 – High Line DP Calibration
Description
This calculates differential pressure generated at line pressure using a twin-post pressure balance (Dead Weight Tester) as the standard. The equation can be solved for either differential pressure or applied mass to generate differential pressure.
The calibration of differential pressure devices at atmospheric pressure (footprint) is effectively a gauge pressure measurement and pressure generated should be calculated using the standard gauge pressure calculation.
References
NPL Report CMAM41 – Development of high-line differential pressure standards (ISSN 1369-6785 – M Hay and D Simpson, 1999)
Kelton calculation reference C192
FLOCALC calculation reference F041
KIMS calculation reference K202
Options
Calculation Method
- Mass and Area
Use this option if you are generating pressure using a twin-post dead weight tester (pressure balance) which is calibrated to give values for mass and effective area.
- Pressure
Use this option if you are generating pressure using a dead weight tester (pressure balance) using a nominal value with corrections.
- Kn
Use this option if you are generating pressure using a twin-post dead weight tester (pressure balance) which is calibrated to give the mass pressure ratio ‘Kn‘.
Solve For
- Differential Pressure
- Applied Mass
Select Applied Mass to calculate the mass required to generate the differential pressure. Selecting Differential Pressure calculates the differential pressure generated by the mass. This option does not appear in the “differential pressure” method.
Correct For
- Temperature
- Gravity
- Line Pressure
- Density of Air
- Density of Mass
Selecting any of these options allows custom values to be entered in place of the default ones.
Temperature
- Single
- Differential
Output Type
- Digital
- Analogue
(Fill in here with the new C numbers)
Calculation
All calculations are carried out in SI units unless otherwise stated.
‘Mass and Area’ method
- If Correct for ‘Density of Mass’ is not selected then a default value of 8000kgm-3 is used.
- If Correct for ‘Density of Air’ is not selected then a default value of 1.2kgm-3 is used.
- If Correct for ‘Temperature’ is not selected then the temperature coefficient (λ) is taken as 0 and the calibration temperature (tc) as 293.15K.
- If Temperature ‘Single’ is selected then initial high PC temperature (tho), initial low PC temperature (tlo), high PC temperature (th) and low PC temperature (tl) are given the default value of 293.15K. Otherwise if ‘Differential’ is selected, the user is able to give custom values to these inputs.
- If Solve for ‘Differential Pressure’ is selected
This equation calculates the differential pressure generated by loading a piston with mass.

- If Solve for ‘Mass’ is selected
This equation calculates the applied mass required to generate pressure.
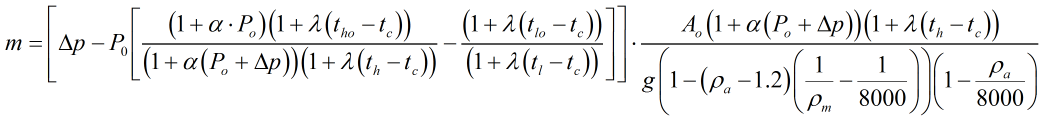
| Where | ||
|---|---|---|
| m | = | Mass used to generate differential pressure |
| Δp | = | Differential pressure |
| Po | = | Line or static pressure |
| ρa | = | Density of air |
| ρm | = | Density of the mass |
| g | = | The local value of acceleration due to gravity |
| Ao | = | Effective area of the piston cylinder unit obtained from calibration |
| α | = | The pressure dependant term for the area of the piston cylinder unit obtained from calibration |
| λ | = | Temperature coefficient of the piston cylinder unit – this is dependant on the materials used in the manufacture of the piston cylinder |
| tc | = | Calibration reference temperature |
| th | = | High piston cylinder temperature |
| tl | = | Low piston cylinder temperature |
| tho | = | Initial high piston cylinder temperature |
| tlo | = | Initial low piston cylinder temperature |
‘Kn’ method
- If Correct for ‘Line pressure’ is not selected then line pressure (Po) = 101325Pa and Pressure Coefficient (α) = 0.
- If Correct for ‘Gravity’ is not selected then the Local gravity and Calibration gravity are given a default value of 9.80665ms-2.
- If Correct for ‘Temperature’ is not selected then temperature coefficient (λ) = 0, calibration temperature (tc) = 293.15K and PC temperature (t) = 293.15K.
- If Solve for ‘Differential Pressure’
This equation calculates the differential pressure generated by loading a piston with mass.

- If Solve for ‘Mass’
This equation calculates the applied mass to generate pressure
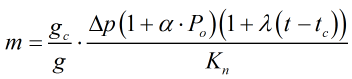
| Where | ||
|---|---|---|
| m | = | Mass |
| Δp | = | Differential pressure |
| Po | = | Line or static pressure |
| g | = | The local value of acceleration due to gravity |
| gc | = | Calibration gravity |
| α | = | Pressure coefficient |
| λ | = | Temperature coefficient |
| t | = | Piston cylinder temperature |
| tc | = | Calibration temperature |
| Kn | = | Pressure ratio |
‘Differential Pressure’ method
- If Correct for ‘Gravity’ is not selected then the Local gravity and Calibration gravity are given a default value of 9.80665ms-2.
- If Correct for ‘Temperature’ is not selected then temperature coefficient (λ) = 0, calibration temperature (tc) = 293.15K and PC temperature (t) = 293.15K.
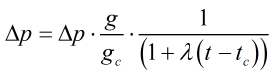
| Where | ||
|---|---|---|
| Δp | = | Differential pressure |
| g | = | The local value of acceleration due to gravity |
| gc | = | Calibration gravity |
| λ | = | Temperature coefficient |
| t | = | Piston cylinder temperature |
| tc | = | Calibration temperature |
