C173 – Wet Gas Venturi Calculation
Description
This calculates the liquid and gas flow rate for a Venturi meter.
References
Kelton calculation reference C173
KIMS calculation reference K179
ISO 5167-1: Measurement of fluid flow by means of pressure differential devices inserted in circular cross-section conduits running full
Flow Measurement Engineering Handbook (2nd Edition) – R.W Miller
Options
Expansibility factor
- User Entered
- Calculated
- Liquid
The expansibility factor can either be user entered, a fixed value of 1 for a liquid or calculated.
Correction
- None
- Murdock
- Chisholm
- User Entered
Select whether the Murdock, Chisholm or user entered correction is to be applied, if the Chisholm correction is applied you will be given the further option of calculating the De Leeuw ‘n’ term.
Discharge Coefficient
- User Entered
- Variable with Reynold’s number
- Classical venturi with ‘as cast’ convergent section
- Classical venturi with machined convergent section
- Classical venturi with rough welded sheet iron convergent section
- Venturi Nozzle
Choose to either enter a fixed value for the discharge coefficient, one which varies with the Reynolds number or use the value which corresponds to the type of Venturi as referred to in the ISO 5167 standard.
Water Density
- User entered
- Calculated
Methanol Densit
- User entered
- Calculated
Note that if there is no methanol present select user entered and enter a non zero term for methanol density otherwise a divide by zero error will occur.
Condensate Density
- User entered
- Calculated
If calculated is selected further options relating to density referral will appear to define how the condensate density is solved.
Standard
- 1991
- 2003
This option allows selection of the relevant version of the ISO 5167 standard to be employed within the calculation.
Exit Cone Angle
- 7°
- 15°
This option is used to select exit cone angle. This uses the calculations set out by in the referenced Handbook by Miller.
Temperature
- Upstream
- Downstream
This option is used to select whether the temperature entered is upstream or downstream of the venturi. If it downstream a correction, dependent on the standard version, will have to be made.
Joule-Thomson
- User entered
- Calculated
If temperature is to be entered downstream and the ISO 5167:2003 is to be used then this option will prompt whether Joule-Thomson coefficient is to be entered by the user or calculated.
Calculations
Expansibility factor
The expansibility factor is calculated using the equation:
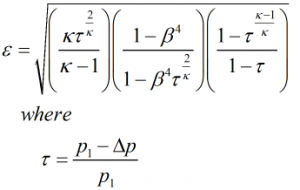
| Where | ||
| κ | = | Isentropic exponent |
| p1 | = | Line pressure |
| Δp | = | Differential pressure |
| β | = | Diameter ratio |
Mass Flow Rate
The general mass flow rate formula from ISO 5167 is used:
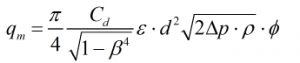
| Where | |||
| Cd | = | Discharge coefficient | |
| β | = | Diameter ratio | |
| ε | = | Expansibility factor | |
| d | = | Throat diameter | |
| ΔP | = | Differential pressure | |
| ρ | = | Density of the fluid | |
| ϕ | = | Wet gas correction factor | |
Chisholm correction
Chisholm correction is calculated from:
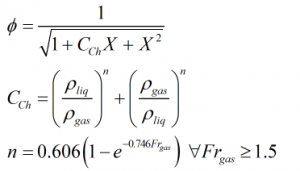
| Where | ||
| ρliq | = | Density of the liquid |
| ρgas | = | Density of the gas |
| Frgas | = | Froude number of the gas |
| X | = | Lockhart-Martinelli parameter |
| n | = | Exponent of Chisholm coefficient, CCh, (n = 0.41 when Frgas < 1.5) |
Murdock Correction
The Murdock correction is calculated from:
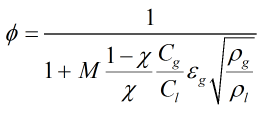
| Where | ||
| M | = | Murdock coefficient |
| Cgas | = | Gas discharge coefficient |
| Cliq | = | Liquid discharge coefficient |
| ε | = | Expansibility factor |
| ρliq | = | Density of the liquid |
| ρgas | = | Density of the gas |
| mliq | = | Mass of the liquid |
| mgas | = | Mass of the gas |
Lockhart-Martinelli Parameter
If ‘include expansibility term’ is selected then the Lockhart-Martinelli parameter is calculated from:
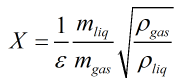
Otherwise the Lockhart-Martinelli parameter is calculated from:
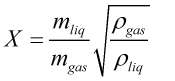
| Where | ||
| ρliq | = | Density of the liquid |
| ρgas | = | Density of the gas |
| mliq | = | Mass of the liquid |
| mgas | = | Mass of the gas |
Permanent Pressure Loss
The permanent pressure loss equations used here have been taken from R.W Miller’s Flow Measurement Engineering Handbook
For a venturi with an exit cone angle of 7°
![]()
For a venturi with an exit cone angle of 15°
![]()
Correction to Upstream Temperature
If the 1991 standard is selected then upstream temperature is calculated by:
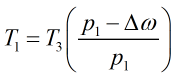
If the 2003 standard is applied:
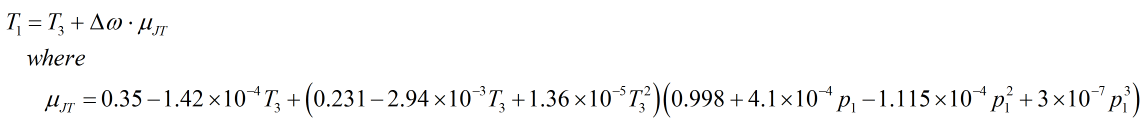
| Where | ||
|---|---|---|
| p1 | = | Upstream pressure |
| κ | = | Isentropic exponent |
| T3 | = | Recovery point temperature |
| Δω | = | Permanent pressure loss |
| μJT | = | Joule-Thomson coefficient |
