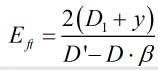C015 – Orifice Plate Buckling
Description
An orifice plate when exposed to differential pressure will always experience a degree of elastic deformation, in certain cases the elastic deformation can be augmented by plastic (permanent) deformation.
This calculates the differential pressure would cause the plastic distortion of a simply supported orifice plate. In addition to this, flow measurement errors caused by the deformation of the orifice plate are estimated.
References
KCCL calculation reference C015
FLOCALC calculation reference F015
Buckling and Eccentricity Effects on Orifice Metering Accuracy, R Norman, M S Rawat and P Jepson (1983)
Effect of Plate Buckling on Orifice Meter Accuracy, P Jepson and R Chipchase Journal Mechanical Engineering Science Vol 17 No 6 (1975)
Options
Calculate
- Maximum DP before yield
- Fractional error on mass flow
- Static error on mass flow
- Total Error on flatness
Select options based on which outputs are required.
Beta Ratio
- User Entered
- Calculated
If calculated is selected the beta ratio is calculated from the orifice and pipe bore (d and D).
Calculations
All calculations are performed in SI units unless otherwise stated.
Coefficients given in the referenced papers are for six values of beta ratio between 0.2 and 0.7, linear interpolation is used to find values within this range.
Maximum DP before yield
This is the highest differential pressure before plasticity occurs.
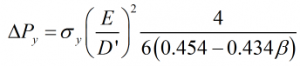
| Where | ||
| E | = | Orifice plate thickness |
| D’ | = | Diameter of the orifice plate at the point where it is supported |
| σy | = | Orifice plate yield stress |
| β | = | Orifice plate beta ratio |
Fractional error on mass flow
The fractional error on mass flow is calculated from:
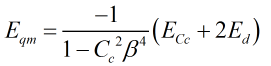
where

and
| K1 2,3 | = | Coefficients from Table 2 |
| a, b | = | Coefficients from Table 3 |
| E | = | Orifice plate thickness |
| E’ | = | Young’s modulus of elasticity |
| Δp | = | Differential pressure across the orifice plate |
| D’ | = | Diameter of the orifice plate at the point where it is supported |
| β | = | Orifice plate beta ratio |
Static error on mass flow
The static error on mass flow is calculated from:
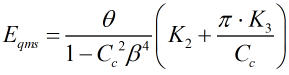
where
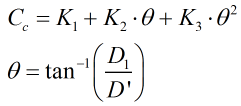
and
| K1,2,3 | = | Coefficients from Table 2 |
| D1 | = | Static deformation |
| D’ | = | Diameter of the orifice plate at the point where it is supported |
| β | = | Orifice plate beta ratio |
Total error on mass flow
This is equal to the sum of the fractional error and the static error.
![]()
Total error on flatness
The total error on flatness is calculated from: