BL-201 – USM – Gas Flow Rate
Description
This block is for a gas ultrasonic meter (USM) where the uncertainty is calculated for volume flow rate, standard volume flow rate, mass flow rate and energy flow rate.
Options
Calibration correction
- None
- Before Spool Correction
- After Spool Correction
This option determines whether calibration corrections are applied before or after spool corrections or not applied at all. Where calibration corrections are applied further options are available as below.
Calibration correction – No. of data points
This is the number of points that form the meter calibration data.
Correction type
- Correction Factor
- Correction Value
- Error (Difference)
- Error (% Actual)
- Error (% Reading)
This is the type of correction to be applied.
Interpolate On
- Absolute Value
- Correction Factor
- % Error
Interpolation between calibration data points can be performed based on absolute value, correction factor or percentage error.
Note: % Error can only be selected with the Error (% Actual) correction type.
Uncertainty calibration correction
- Fixed
- Variable with flow rate
Calibration uncertainty can be selected as a fixed value or variable with flow rate.
Inputs
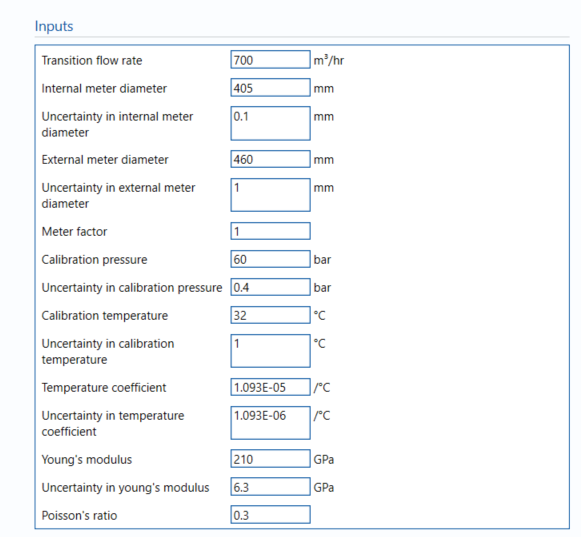
Transition flow rate
The transition flow rate of the USM. This is determined by the meter manufacturer and is the point below which the performance requirements are relaxed.
Internal meter diameter
The internal diameter of the USM.
Internal meter diameter
The internal diameter of the USM.
Uncertainty in internal meter diameter
Uncertainty in the measurement made of the meter’s internal diameter
External meter diameter
The external diameter of the USM.
Uncertainty in external meter diameter
Uncertainty in the measurement made of the meter’s external diameter
Meter factor
Enter the meter factor for the USM.
Note: If the meter factor is not given input 1.
Calibration pressure
Pressure at which the meter has been calibrated.
Uncertainty calibration pressure
Uncertainty in the reading of the calibration pressure.
Calibration temperature
Temperature at which USM measurement was made.
Uncertainty calibration temperature
Uncertainty in the reading of the calibration temperature.
Temperature coefficient
Temperature expansion coefficient is the change in physical property over a change in temperature that causes it.
Uncertainty in temperature coefficient
Uncertainty in the value of the temperature coefficient.
Young’s modulus
Enter Young’s modulus.
Note: Young’s modulus is the ability of material to withstand tension or compression.
Uncertainty in Young’s modulus
Uncertainty in the value of Young’s modulus.
Poisson’s ratio
Enter Poisson’s ratio.
Note: Poisson’s ratio is the ratio between transverse strain and longitudinal strain in the direction of the force applied.
Uncertainty Parameters
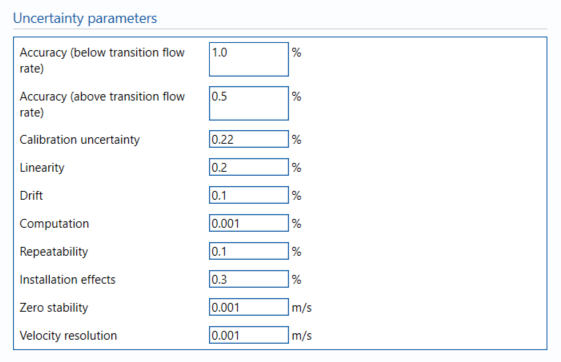
Accuracy (below transition flow rate)
Enter the percentage uncertainty due to accuracy below the transition flow rate.
Accuracy (above transition flow rate)
Enter the percentage uncertainty due to accuracy above the transition flow rate.
Calibration uncertainty
Enter the percentage uncertainty due to calibration, if a fixed value is used.
Note: If the calibration uncertainty is selected as variable with flow rate, the calibration uncertainty for each data point is entered in the input tables.
Linearity
Enter the percentage uncertainty due to linearity. Linearity is calculated by getting the average and the range of the measurements made. The sample averages and ranges will be used with the reference values to determine linearity either graphically or by calculations.
Drift
Additional uncertainty allowance due to meter drift from factors such as time, ambient temperature and line voltage. Normally left at zero, unless evidence is present to suggest a higher value.
Note: Drift is rarely apparent but needs to be continuously monitored through inspection, prevention and maintenance.
Computation
Uncertainty due to computational errors in flow computer.
Repeatability
Enter repeatability percentage. Repeatability is the variation of measurement by an instrument on the same item.
Installation effects
Enter the percentage uncertainty due to installation effects. Installation effects can be from several sources such as a distorted swirl in the profile of the flow due to the layout of the piping system.
Uncertainty Budget
Volume flow rate
The uncertainty budget table shows a break down of the different components that contribute to the overall calculated uncertainty.
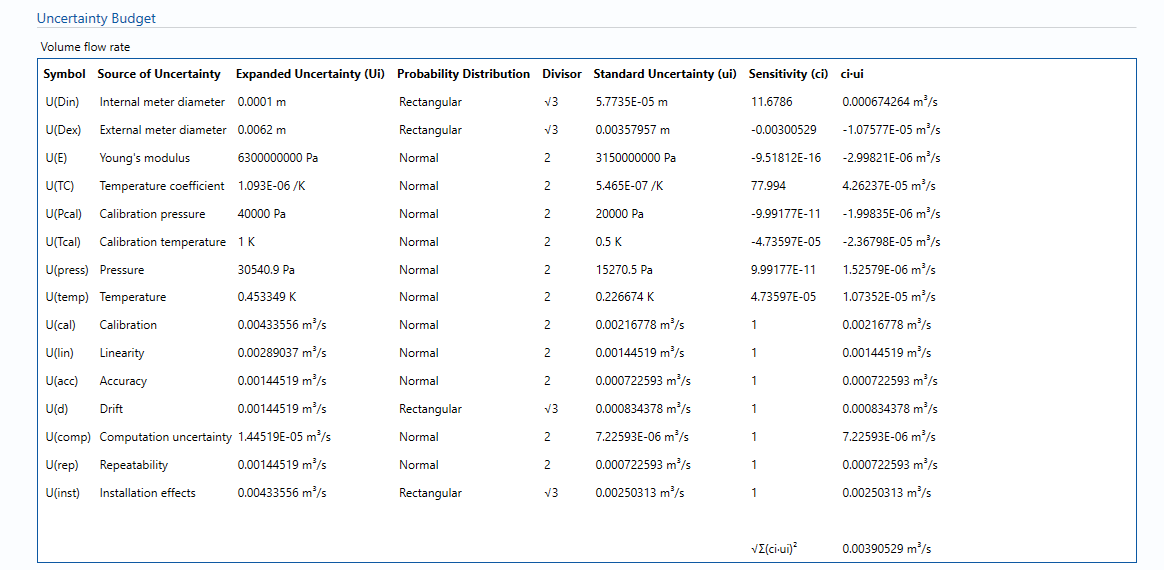
The values input into the uncertainty budget are derived from the measured pressure and the transmitter specific values relating to its calibration and specification. These values are taken in as the expanded uncertainties and are divided by a coverage factor to gain the standard uncertainty.
The coverage factor is determined by the probability distribution that best suits that uncertainty component. The standard uncertainty is then multiplied by the sensitivity value then squared. This is done for each component that contributes to the overall uncertainty in Volume flow rate. The Standard Uncertainty in volume flow rate is the square root of the sum of each component variance as shown in the following equation:
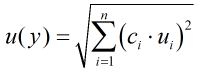
Standard volume flow rate
The uncertainty budget table shows a break down of the different components that contribute to the overall calculated uncertainty.

The values input into the uncertainty budget are derived from the measured pressure and the transmitter specific values relating to its calibration and specification. These values are taken in as the expanded uncertainties and are divided by a coverage factor to gain the standard uncertainty.
The coverage factor is determined by the probability distribution that best suits that uncertainty component. The standard uncertainty is then multiplied by the sensitivity value then squared. This is done for each component that contributes to the overall uncertainty in standard volume flow rate. The Standard Uncertainty in the standard volume flow rate is the square root of the sum of each component variance as shown in the following equation:
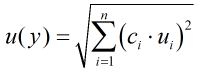
Mass flow rate
The uncertainty calculation for the mass flow rate is detailed in the uncertainty budget table giving a break down of how the overall uncertainty is calculated. The values input into the uncertainty budget are taken from the module inputs and calculations from other blocks along with the uncertainty components calculated in this block from the calculation inputs.

The coverage factor is determined by the probability distribution that best suits that uncertainty component. The standard uncertainty is then multiplied by the sensitivity value then squared. This is done for each component that contributes to the overall uncertainty in mass flow rate. The Standard Uncertainty in mass flow rate is the square root of the sum of each component variance as shown in the following equation:
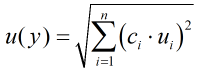
Energy flow rate
The uncertainty budget table shows a break down of the different components that contribute to the overall calculated uncertainty.

The values input into the uncertainty budget are derived from the blocks used in the module relating to its calibration and specification. These blocks are taken in as the expanded uncertainties and are divided by a coverage factor to gain the standard uncertainty.
The coverage factor is determined by the probability distribution that best suits that uncertainty component. The standard uncertainty is then multiplied by the sensitivity value then squared. This is done for each component that contributes to the overall uncertainty in energy flow rate. The Standard Uncertainty in energy flow rate is the square root of the sum of each component variance as shown in the following equation:
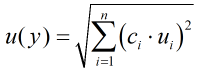
Calculated Uncertainty

The Expanded Uncertainty is the Standard Uncertainty multiplied by the coverage factor (k). The coverage factor is defaulted to k = 2 (equivalent to a confidence level of approximately 95%).
The Relative Uncertainty is the Expanded Uncertainty divided by the mass flow rate or standard volume flow rate or energy flowrate depending on the parameter.
References
Standards
ISO 5168:2005 – Measurement of fluid flow – Procedures for the evaluation of uncertainties
ISO Guide 98-3 – Uncertainty of measurement – Part 3: Guide to the expression of uncertainty in measurement (GUM:1995)
