BL-121 – Liquid Volume Prover
Description
This block calculates the uncertainty in the inferred mass proving method. The overall uncertainty for prover base volume as well as mass is calculated.
Volume prover
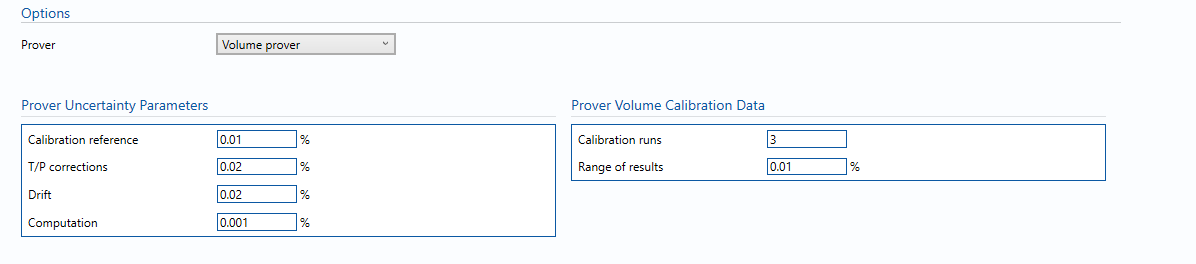
Prover Uncertainty Parameters
- Calibration reference – Uncertainty in calibration reference device.
Note: For example this could be water draw or gravimetric system.
- T/P corrections – Uncertainty due to temperature and pressure corrections for prover during prover calibration.
- Drift – Maximum drift in prover volume between calibrations.
Note: Can only get this from repeat calibration data.
- Computation – Uncertainty due to computational errors in flow computer.
Note: Negligible term included for completeness – assume 0.001%.
Prover Volume Calibration Data
- Prover Base Volume – The base volume of the prover.
- Calibration runs – Number of consecutive calibration runs used to determine the average prover volume.
Note: Default (and suggested minimum) is 3 runs.
- Range of Results – The range between the maximum and minimum prover volumes obtained in individual runs.
Calculations
Prover Volume flow rate
The uncertainty calculation for the prover base volume and inferred mass is detailed in the uncertainty budget tables giving a break down of how the overall uncertainty is calculated.
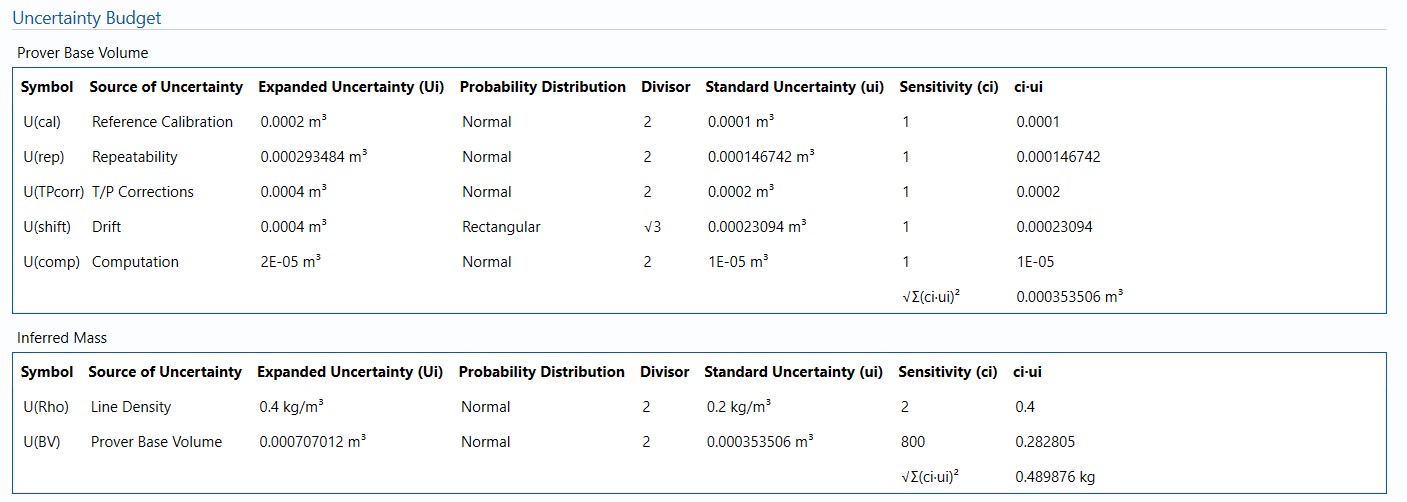
The values input into the uncertainty budget are taken from the uncertainty components calculated in this block from the calculation inputs. These values are taken in as the expanded uncertainties and are divided by a coverage factor to gain the standard uncertainty.
The coverage factor is determined by the probability distribution that best suits that uncertainty component. The standard uncertainty is then multiplied by the sensitivity value then squared. This is done for each component that contributes to the overall uncertainty in prover base volume/inferred mass. The Standard Uncertainty in prover base volume/inferred mass is the square root of the sum of each component variance as shown in the following equation:
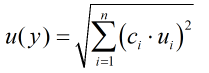
Calculated Uncertainty

The Expanded Uncertainty is the Standard Uncertainty multiplied by the coverage factor (k). The coverage factor is defaulted to k = 2 (equivalent to a confidence level of approximately 95%).
The Relative Uncertainty is the Expanded Uncertainty divided by the prover base volume/inferred mass depending on the parameter.
References
Standards
ISO 5168:2005 – Measurement of fluid flow – Procedures for the evaluation of uncertainties
ISO Guide 98-3 – Uncertainty of measurement – Part 3: Guide to the expression of uncertainty in measurement (GUM:1995)
