B005 – Calculated Gas Density
Description
This block calculates the uncertainty in gas density determined by the detail characterisation method presented in AGA Report No. 8. The detail characterisation as per the 1994 option is used in ISO 12213.
Options
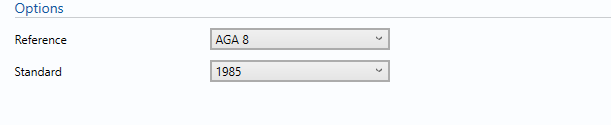
Reference
AGA 8 is the reference used by KELTON UNCERTAINTYPLUS to compute the gas density.
Standard
- 1985
- 1994
This option determines which version of AGA 8 is used for the calculation of density.
Add neo-Pentane to
![]()
- i-Pentane
- n-Pentane
This option is used to determine which component any neo-pentane will be added to.
Note: this option is available only for the 1994 standard.
Equation of State Uncertainty
- User Entered
- Calculated
The uncertainty in the equation of state can be calculated from the pressure, temperature and composition ranges presented in AGA Report No. 8 or can be user entered.
Inputs

Uncertainty in equation of state for line density
Uncertainty in the equation of state. Guidelines on determining this value can be found in the relevant standard.
Note: that the uncertainties given in AGA8:1994, Figure 1 are only valid for the “normal” range of compositions given in the standard; for compositions in the “extended” range the uncertainty will be higher, but the standard does not specify how much higher. Engineering judgement should be used here, however it is recognised that this is difficult at best, due to lack of data.
Calculations
The gas composition and its individual uncertainties are taken from the block B004 – Composition. The pressure and temperature will be taken from the Input/output tab and the expanded uncertainties used will be as calculated in blocks B001 – Pressure and B003 – Temperature respectively.
Uncertainty Budget
The uncertainty calculation is detailed in the uncertainty budget table giving a break down of how the overall uncertainty is calculated. The values input into the uncertainty budget are taken from the module inputs and calculations from other blocks along with the uncertainty in the equation of state as input in this block.
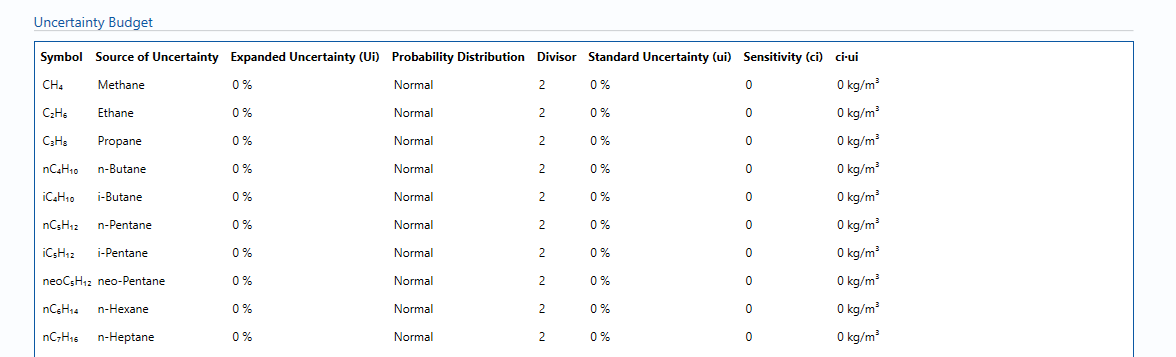
Uncertainties associated with these values are taken in as the Expanded Uncertainties. The Standard Uncertainty is calculated from dividing the Expanded Uncertainty by the coverage factor which is determined by the probability distribution that best suits that uncertainty component.
The standard uncertainty is then multiplied by the sensitivity value then squared. This is done for each parameter that contributes to the overall uncertainty in gas density. The Standard Uncertainty in gas density is the square root of the sum of each component variance as shown in the following equation:
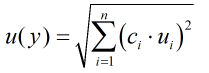
Note: The sensitivity coefficients for each of these input uncertainties are determined using the finite difference method, where each of the calculation input quantities are varied, one at a time, by magnitude of their uncertainty, and the effect on the output determined.
Calculated Uncertainty

The Expanded Uncertainty is the Standard Uncertainty multiplied by the coverage factor (k). The coverage factor is defaulted to k = 2 (equivalent to a confidence level of approximately 95%).
The Relative Uncertainty is the Expanded Uncertainty divided by calculated Gas density.
References
Standards
ISO 5168:2005 – Measurement of fluid flow – Procedures for the evaluation of uncertainties
ISO Guide 98-3 – Uncertainty of measurement – Part 3: Guide to the expression of uncertainty in measurement (GUM:1995) (2008)
AGA Report No. 8 – Compressibility and Supercompressibility of Natural Gas and Other Related Hydrocarbon Gases (December 1985)
AGA Report No. 8 – Compressibility Factors of Natural Gas and Other Related Hydrocarbon Gases (2nd Printing July 1994)
ISO 12212-2:2006 – Natural Gas – Calculation of compression factor – Part 2: Calculation using molar composition analysis
KCCL Calculations
C156 – AGA8 1985/94 – Gas Density and Compressibility
